سطح دوراني

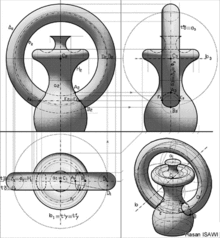
السطح الدوراني يتولد من دوران خط g (مستقيم أو منحني) حول خط مستقيم ثابت a، في هذة الحالة نطلق على الخط المتحرك g راسم السطح وعلى a محور الدوران.^[1]^[2]^[3] يجب الأخذ بعين الاعتبار ان معظم أنواع السطوح الدورانية تنتج في حالة انتماء الخطوط g a إلى نفس المستوى (complanari)

المنحني الذي يتم الحصول علية كنتيجة لتقاطع السطح الدوراني بسطح عمودي على محور الدوران، يسمى منحني موازي (Parallel)
المنحني الذي يتم الحصول علية كنتيجة لتقاطع السطح الدوراني بسطح يمر بمحور الدوران، يسمى منحنى الطول (Longitude)

أنواع

حسب طبيعية راسم السطح g (مستقيم أو منحني), تتولد السطوح التالية:

1- في الحالة التي يكون فيها g خط مستقيم (conica degenere), السطح الدوراني الناتج هو:
- - مخروط عندما g يتقاطع مع a في نقطة V حقيقية
- - اسطوانة عندما g يتقاطع مع a في نقطة V∞ خيالية
2- في الحالة التي يكون فيها g منحنى، السطح الناتج هو:

- سطح ثنائي دوراني، عندما تكون g مقطع مخروطي (اهليج، قطع مكافئ، قطع زائد)، وبحيث يكون محور الدوران متطابق مع محور من محاور القطع المخروطي^[4] - سطح دوراني عام، عندما تكون g أي نوع من المنحنيات التي لم يسبق ذكرها.